A Middling and Situational Sort
Part of my personal projects using C is that there is a fair few bits of code that are broadly useful to me, and potentially others, across many current and future repositories.
The initial, naive, quick and dirty approach I often start out with is to just copy a piece of code I am using between projects, fine on that small scale and if you know changes are not going to have to be passed back and forth, but as soon as you want to share improvements and changes between projects, immediate hassle.
Submodule(s), especially with CMakeLists set up for them, is how I have massively lubricated the use of shared code. For the most part I have just been putting anything broad and polished enough that I feel happy with it being all over the place, at least right now. I’m sure in a decade I’ll either despise it all as amateurish garbage that I regret sharing or I will have been obsessively reworked the whole thing a dozen times by that point.
Isolated in their own repo their focus can remain the supreme functionality, I can’t end up repeating myself, and I can’t unintentionally tie it to something less portable. In addition, given the form that this now fits it easily shared in a useful form, for that OSS cred. I am more than happy if people want you use this for their own projects, if you want to; let me know, I want to see what cool stuff people are working on. Keep in mind it is somewhat GCC focused, I may rectify this in future but don’t rely on it.
This is a collection of things like a string hashing function that can run at compile time if needed, some functions that give you the number of digits a number has given a couple of different common bases, and a type agnostic swap macro. I’m pretty happy with that last one:
#define swap_helper(_1, _2, _3, NAME, ...) NAME
#define swap_known(a,b) \
do { \
__typeof__ (a) _a = (a); \
__typeof__ (b) _b = (b); \
if (_a == _b) break; \
unsigned char swap_temp[sizeof(*_a) == sizeof(*_b) ? (signed)sizeof(*_a) : -1]; \
memcpy(swap_temp,_b,sizeof(*_a)); \
memcpy(_b,_a,sizeof(*_a)); \
memcpy(_a,swap_temp,sizeof(*_a)); \
} while(0)
#define swap_size(a,b,size) \
do { \
__typeof__ (a) _a = (a); \
__typeof__ (b) _b = (b); \
__typeof__ (size) _size = (size); \
if (_a == _b) break; \
unsigned char swap_temp[_size]; \
memcpy(swap_temp,_b,_size); \
memcpy(_b,_a,_size); \
memcpy(_a,swap_temp,_size); \
} while(0)
#define swap(...) swap_helper(__VA_ARGS__, swap_size, swap_known)(__VA_ARGS__)
It sits somewhere in my mind like the prettiest, most handsome, goblin. It feels like a mess but is relatively clean, very capable, and able to handle arbitrary sizes of data. Still, like with a lot of what I put up; if you have suggestions for improvements do let me know.
The focus of this act of coding will remain primarily for the benefit of my own projects, so what I currently need gets the grease.
It is worth acknowledging that in this realm lies madness, all should be weary as to not let it overtake you. There is 2 ends to this spectrum; ‘Not invented here’ syndrome and ‘proudly found elsewhere’ are both common pitfalls, as always, balance is key. I have often fell into the latter, I have built a software render for 3D multiple times.
Anyway that is all an aside to some experimentation that I have done within the submodule. Sorting algorithms are hardly untrod ground but I still thought it was worth poking into the possibilities for novelty. Nothing too original you understand, just bits and pieces in the details, like a bitwise focus for a In-place MSD binary-radix sort, or looking into the use of data ‘rotations’ to reduce memory usage.
As part of my testing and evaluation of these different algorithms it made sense to be able to measure the real world performance of the algorithms so that I could, at the very least, can discern if there was any actual improvements.
The following is a table showing in microseconds how long it takes for the a list of a given size/length to be sorted 100 times by each algorithm, for lengths 1 to 10000 entries long. While all 10000 lengths have been tested the table on this page are just those at regular intervals for readability in this format.
| Array size | stdlib qsort | quicksort_Lomuto | quicksort_Hoare | insertionSort | binaryInsertionSort | mergeSort | mergeSort_inPlace | heapSort | binaryRadixSort_lsd | binaryRadixSort_lsd_inPlace | binaryRadixSort_msd |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 1 | 1 | 2 | 1 | 1 | 3 | 2 | 13 | 3 | 5 |
| 2 | 4 | 14 | 24 | 11 | 14 | 15 | 13 | 17 | 9 | 12 | 12 |
| 3 | 15 | 14 | 29 | 13 | 26 | 25 | 19 | 37 | 12 | 21 | 17 |
| 4 | 18 | 33 | 50 | 24 | 36 | 37 | 28 | 68 | 18 | 36 | 30 |
| 5 | 24 | 41 | 73 | 56 | 49 | 55 | 65 | 87 | 31 | 61 | 45 |
| 6 | 36 | 65 | 105 | 104 | 75 | 67 | 69 | 163 | 30 | 92 | 54 |
| 7 | 40 | 64 | 115 | 139 | 84 | 71 | 80 | 397 | 38 | 87 | 72 |
| 8 | 29 | 40 | 99 | 118 | 90 | 82 | 85 | 222 | 38 | 92 | 75 |
| 9 | 26 | 42 | 109 | 149 | 97 | 113 | 124 | 234 | 64 | 177 | 99 |
| 10 | 44 | 62 | 148 | 159 | 118 | 141 | 156 | 256 | 73 | 169 | 102 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 20 | 68 | 167 | 277 | 635 | 316 | 356 | 415 | 824 | 194 | 401 | 323 |
| 30 | 59 | 144 | 215 | 367 | 161 | 176 | 184 | 365 | 160 | 189 | 211 |
| 40 | 109 | 252 | 353 | 673 | 275 | 403 | 320 | 597 | 288 | 331 | 311 |
| 50 | 142 | 397 | 422 | 1219 | 289 | 334 | 378 | 756 | 352 | 435 | 493 |
| 60 | 148 | 474 | 547 | 1916 | 401 | 514 | 552 | 1059 | 425 | 546 | 543 |
| 70 | 185 | 483 | 580 | 1884 | 408 | 513 | 610 | 1106 | 531 | 680 | 607 |
| 80 | 228 | 587 | 736 | 2922 | 571 | 649 | 842 | 1512 | 653 | 1041 | 1179 |
| 90 | 320 | 700 | 909 | 3596 | 658 | 770 | 955 | 1548 | 721 | 904 | 860 |
| 100 | 306 | 874 | 1019 | 4078 | 684 | 829 | 1093 | 2039 | 810 | 1199 | 911 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 200 | 1120 | 2642 | 3101 | 22747 | 2178 | 2052 | 2747 | 4357 | 1788 | 3122 | 2589 |
| 300 | 1745 | 3738 | 4263 | 40598 | 3876 | 3610 | 4866 | 9053 | 3465 | 5793 | 4095 |
| 400 | 2309 | 4765 | 5019 | 63793 | 4489 | 5480 | 6736 | 10660 | 3949 | 7180 | 5071 |
| 500 | 2828 | 6730 | 7400 | 108658 | 6643 | 6389 | 9124 | 13153 | 5361 | 10604 | 7229 |
| 600 | 4813 | 8992 | 8673 | 172244 | 8290 | 8104 | 10828 | 17030 | 6872 | 13145 | 8725 |
| 700 | 5605 | 10654 | 9707 | 199035 | 10017 | 12441 | 14059 | 20570 | 8093 | 18585 | 10615 |
| 800 | 5919 | 12071 | 11121 | 241238 | 11497 | 10406 | 13986 | 22166 | 8775 | 19626 | 12291 |
| 900 | 6262 | 13446 | 12037 | 310440 | 12245 | 11442 | 15602 | 24300 | 10348 | 20592 | 12394 |
| 1000 | 7069 | 12926 | 14034 | 410103 | 14762 | 13342 | 22623 | 29822 | 11302 | 28987 | 15897 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2000 | 18195 | 36940 | 31622 | 1597374 | 37231 | 29680 | 48613 | 71416 | 25120 | 85398 | 32914 |
| 3000 | 28637 | 56034 | 52639 | 3849109 | 66713 | 47449 | 89457 | 112360 | 46197 | 198895 | 53517 |
| 4000 | 44701 | 87685 | 81478 | 9071724 | 136827 | 85207 | 166422 | 217025 | 71577 | 431511 | 111808 |
| 5000 | 52737 | 104062 | 95727 | 11328517 | 148815 | 90130 | 182635 | 204126 | 75504 | 517301 | 98491 |
| 6000 | 81017 | 133644 | 147003 | 22783986 | 256091 | 117588 | 441152 | 462076 | 95890 | 846814 | 161725 |
| 7000 | 74284 | 152268 | 131168 | 21390353 | 243164 | 124133 | 275194 | 288889 | 107165 | 933076 | 137430 |
| 8000 | 88528 | 169494 | 150693 | 28530726 | 310638 | 155700 | 364241 | 370142 | 121009 | 1225565 | 164575 |
| 9000 | 100774 | 186938 | 167816 | 33929186 | 346937 | 166376 | 408429 | 375812 | 137098 | 1413708 | 177755 |
| 10000 | 115117 | 227681 | 181148 | 38266663 | 399948 | 175163 | 451764 | 412896 | 153328 | 1730489 | 189457 |
The full set of results, collected continuously over several days, can be found here: https://gist.github.com/MegaDarken/0f8186aa7c84c9fc684d9f3874daec9a
Even in this form there is some thing I think it is fair to say that some outside factors had an influence in parts of this as sections will jump down and jump up.
I was pleasantly surprised with how well binaryRadixSort_lsd did on the high end, it has similar memory usage to the iterative merge sort O(n) space, but appears to outperform it. Related; the in-place variants of those same algorithms are both slower, as you may expect, but they have the opposite relationship, the in-place merge sort is faster than the in-place binaryRadixSort_lsd. I’m fairly certain this is because the rotations used to make the algorithms not require additional memory work by shifting blocks of data around, the further the distance between values moved the more data has to be moved, and while the mergesort movements tend to keep relatively localized, while binaryRadixSort_lsd
From this data we can make some graphs:
All sorts to 10000:
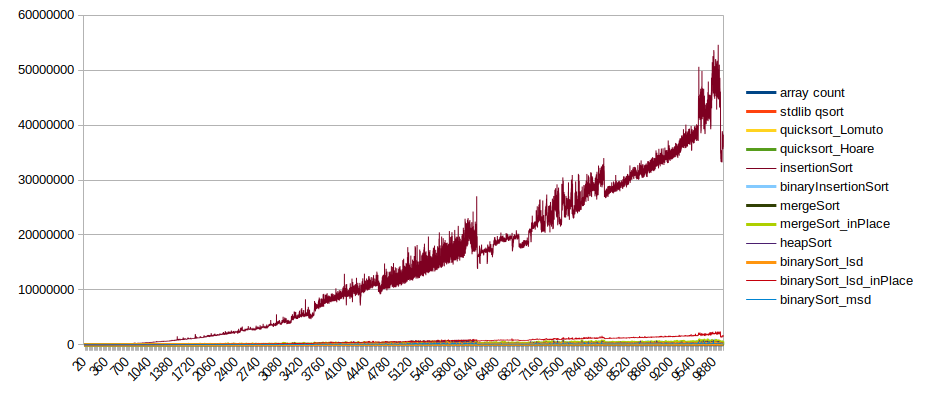
The same without insertion sort:
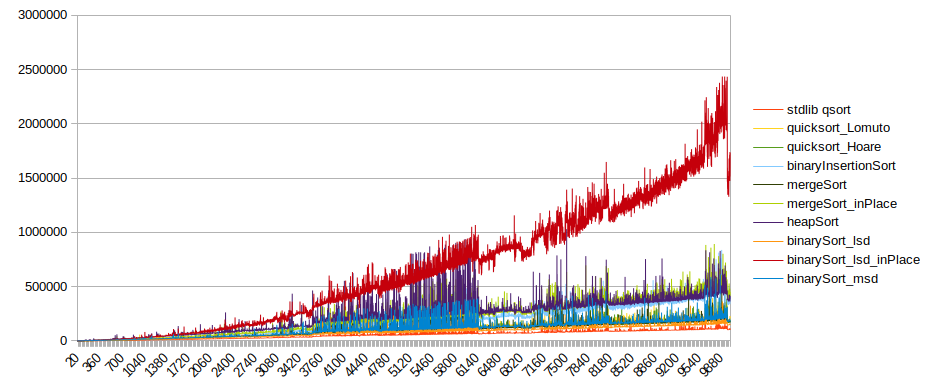
The same without insertion sort or binaryRadixSort_lsd_inPlace:
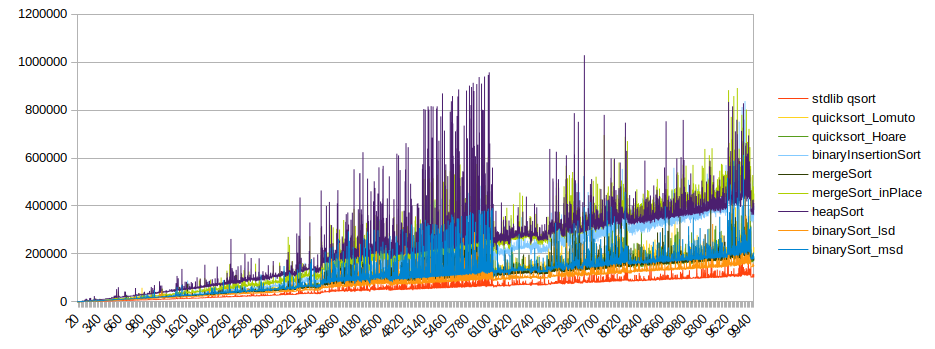
I’m sure others can graph this better than I have.
Was this massively overkill? Seems like it.
The algorithms that are functional enough should be able to be found in the Shared-C repo, linked above.